TECNICHE PARTICOLARI NELL'INIZIO


DEL LAVORO DI SMODELLATURA





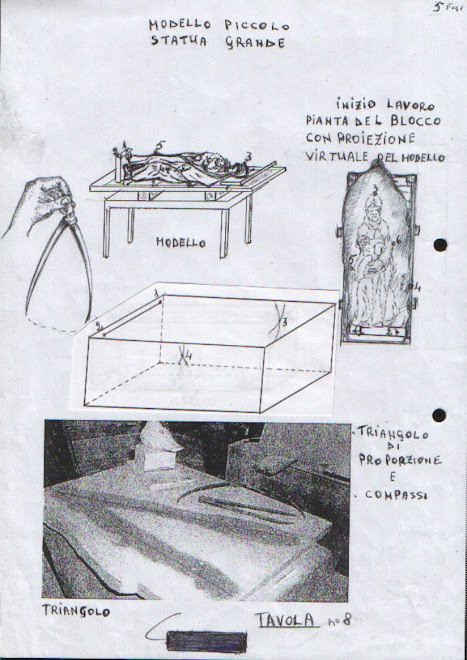
Sul triangolo rettangolo.

Abbiamo già indicato – sulla sbozzatura/smodellatura – diverse tecniche in merito all'inizio lavoro, citandone l'impiego, anche sul triangolo isoscele e descrivendo le specifiche valenze di ognuno, con i relativi tempi di applicazione; e, nell'insieme, riguardanti statue di medie e piccole dimensioni. Le osservazioni che seguiranno, le dedicheremo a misure più grandi, colossali, di cinque o più metri.

Consideriamo l'ipotesi di una statua di m 5 ed un modello di m 1, equivalenti a cm 500 e cm 100 : i compassi ed il maranghino, quando si confrontano con queste misure possono essere imprecisi e poco maneggevoli. I piani di rilievo, alla superficie od alla base vanno individuati, sia con i tre punti sia con le linee proiettive: i loro problemi sono costituiti dalle dimensioni del lavoro e del triangolo.

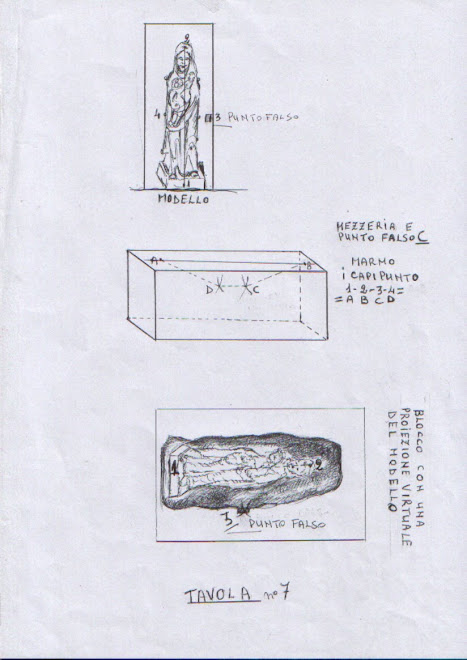
Quando ingrandiamo o rimpiccioliamo una figura, operiamo in modo da mantenere inalterati tutti gli angoli del modello, mentre tutti i suoi segmenti vengono aumentati o diminuiti in proporzione: in definitiva non facciamo altro che costruire una figura simile al modello. Nel nostro caso, il termine figura, è riferito propriamente al complesso delle sembianze umane, oppure alla forma o aspetto esterno di qualche cosa: da fingere “plasmare” e nel significato tridimensionale di studio delle figure solide. Così nello scolpire il tutto è riconducibile ad una schematica immagine di forme geometriche: composizioni e fattezze particolarmente utili nella fase di sbozzatura. Operiamo trasformazioni di figure aventi la stessa forma, perciò simili. Nell'utilizzo della similitudine dei triangoli, essi lo sono, quando hanno la stessa forma e hanno gli angoli ordinatamente uguali, mentre i lati corrispondenti sono in proporzione. Quindi, possiamo definire la regola nelle riproduzioni in scala: ogni parallela ad uno dei lati di un triangolo, o angolo di proporzione, che intersechi gli altri due, determina con questi ultimi un triangolo simile a quello dato e divide gli altri due lati in segmenti direttamente proporzionali; anche la stessa parallela mantiene lo stesso rapporto con il suo corrispondente. Infatti dato un triangolo ABC, in qualsiasi punto del suo lato AB, se conduciamo la parallela DE al lato BC, avremo i lati corrispondenti in proporzione: AB: AD = AC: AE = BC: DE. Cioè siamo interessati ad un problema geometrico:: dividere una retta data nella stessa proporzione in cui è divisa un'altra retta data; così come lo è la divisione di due o più segmenti, riferiti alla stessa unità di misura, in parti tra loro congruenti. Ad esempio dividiamo le altezze del modello e della statua per uno stesso divisore: ( cm 500: 2 = cm 250 ) e ( cm 100: 2 = cm 50 ), avremo da gestire due misure ridotte, fra loro direttamente proporzionali, che ci consentono di lavorare, sia segnando il triangolo in un lastra; sia, come precedentemente descritto, segnando la mezzerie delle figure e mettendo ai loro fianchi il terzo e quarto capo-punto, fatti salvi gli spessori esistenti. Abbiamo indicato questa impostazione del piano, come quella del “punto falso “ , ciò però non esclude altri approcci, già esplorati; ma è nostra convinzione che questa preparazione, del terzo punto di servizio, sia la più facile: poiché abbiamo una linea longitudinale di mezzeria ed il controllo delle fiancate, con un piano a piacere che ci consente di controllare meglio il lavoro.

Una ulteriore considerazione, dopo aver fissato il capo-punto 3: il lavoro procede con relativa facilità, perchè le misure e l'apertura dei compassi si riducono ulteriormente, fissando, da subito, il capo-punto 4 nell'altra faccia del marmo.



Possiamo ridurre ancora, eccovi altri esempi, le misure del triangolo di proporzione e, considerate quelle del marmo in cm 501 e quella del modello di cm 102, le dividiamo per tre. Troveremo due soluzioni corrispondenti. La prima, identica procedura dell’esempio precedente, dividiamo per tre marmo e modello : l'uno cm 501:3 = cm 167, l'altro cm 102:3 = cm 34 . In questo caso per misure maggiori, prese dal modello, superiori a cm. 34, possiamo usufruire del prolungamento delle semirette.
La seconda, può verificarsi come un'eccezione utile alla regola, lasciando inalterata la misura del modello, che rimane com'è, segnando sul triangolo cm 102. Possiamo farlo con qualsiasi grandezza, dividendendo solamente quella della statua (cm 501) : cioè dividiamo per 3 il lato più lungo, che assume il ruolo guida, l’ipotenusa, di cm 501:3= cm 167, adottando un particolare accorgimento; dopo aver rilevato una misura dal modello e sviluppata proporzionalmente con l'arco tangente, se, poniamo occasionalmente, il risultato è di cm 75, dobbiamo moltiplicarla per tre ( cm 75x3 = cm 225 ), che sarà la lunghezza reale da trasportarsi sul blocco, ristabilendo la congruità o valore sottratto dalla divisione iniziale.



Occorre far molta attenzione nel caso di statue colossali, soprattutto se riprodotte da modelli molto piccoli: le riduzioni del triangolo, dianzi dette, mantengono una loro validità se utilizziamo, rispondendo alle difficoltà di un lavoro, sia la scala numerica, sia il sistema delle scale grafiche o ticoniche. Comunque, entrambe sono utili nel determinare più esattamente, anche con due letture, le proporzioni poste.

Un sistema pratico è quello di dividere, in un egual numero di parti uguali, le altezze della statua e del modello, con la certezza di una proporzionalità evidente e corrispondente; ma vi è un altra importante congruità, che vedremo in altra specifica tesi, nella stessa divisione delle altezze tra statua e modello. Per ora, prendiamo le misure dianzi considerate: cm 501 e 102, dividiamole per 10 (o altro denominatore): avremo cm 50,1 e cm 10,2 che sono proporzionali o congrui tra di loro. Poiché ad ogni cm 10,2 del modello corrispondono, in scala, cm 50,1 della statua. E' possibile dividere ancora una parte di quel 10% ( 1/10 ), fino a misure infinitesimali. Ma è consigliabile, una volta esperite le prime suddivisioni uguali ed unitarie, costruire e servirsi del triangolo di proporzione.



IL RAPPORTO PREFERENZIALE

SCALE NUMERICHE E GRAFICHE

LE SCALE DI PROPORZIONE possono essere NUMERICHE O GRAFICHE.
LA SCALA DI PROPORZIONE è il rapporto tra le misure lineari del disegno e le corrispondenti dell'oggetto reale che si deve rappresentare graficamente. Nel nostro lavoro l'oggetto è il modello/statua, qualche volta espressi da un disegno. La scala numerica è indicata con una frazione (1:10, 1:50, 1:100 ecc.).Il primo termine (numeratore) indica l'unità di misura nel disegno; Il secondo (denominatore) quante volte l'unità di misura corrisponde alla realtà.
La scala grafica semplice si costruisce tracciando una retta, sulla quale si riportano tante suddivisioni uguali come abbiamo già indicato.
Si è richiamato queste elementari nozioni per introdurre una novità nel lavoro di smodellatura e nell'utilizzo dell'angolo o triangolo di proporzione. Cioè affronteremo, in seguito, un particolare rapporto di similitudine, che ci faciliti la riduzione o l'ingrandimento in scala di una scultura,con un valore costantemente evidenziato, tra lati corrispondenti, che si definisce rapporto di similitudine.
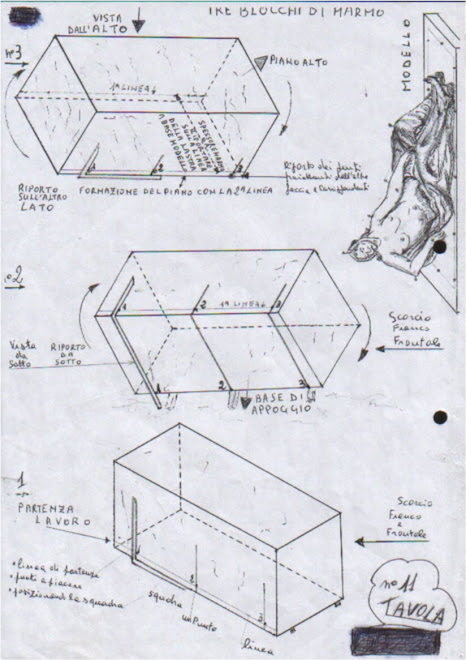
In una statua di grandi dimensioni, per fissare alcuni iniziali capi-punto, è utile ridurre le misure a grandezze ragionevoli, per far si che l'apertura dei compassi sia alla portata di ogni lavorante: I maranghini lascino ai compassi, più piccoli, il compito di confrontarsi con misure dimezzate e campi di smodellatura sempre più brevi ( minori di un 1 metro ), nei quali i puntatore possa operare con sicurezza e maestria con compassi sempre più piccoli e maneggevoli. In statue dai 5 o 6 metri, è ancora possibile fissare un capo-punto intermedio, considerando che un maranghino può attuare misure precise intorno ai 3 metri e mezzo. Nella pratica comune si traccia nel modello e nel blocco la linea di mezzeria e fissati all'estremità di essa i due capi punto iniziali, uno alla testa e l'altro ai piedi della statua, si riportano prima su un fianco, poi sull'altro (di fronte), il 3° e 4° capo-punto. Di seguito si riportano tutti gi altri che sono molteplici ( una costellazione), come ampiamente spiegato nelle "Tesi".

IL QUOZIENTE DI DIVISIONE: Funzione rappresentativa della proporzionalità diretta.

Due grandezze se sono direttamente proporzionali il rapporto fra un qualunque valore della prima ed il corrispondente valore della seconda è costante, Y : X = a, ossia Y = a.x . Evidentemente se 1 cm cubo di marmo pesa g. 3, evidentemente 2 cm cubi peseranno 6 g, 3 uguale 9, e così via.

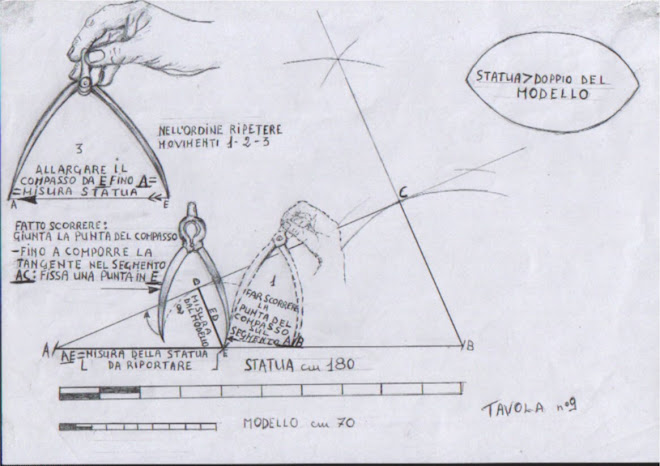
In questa tesi siamo intressati ad un particolare rapporto preferenziale,quello di due lati corrispondenti di poligoni simili che hanno sempre lo stesso valore: tale rapporto si dice rapporto di similitudine. Le due altezze, nel triangolo di proporzione, quella della statua e del modello, mantengono un valore costante. Come utilizzarlo? Siamo altresì interessati ad un quoto possibilmente intero e con minor numeri infinitesimali; ma se si verifica il problema è facilmente superabile con una modesta calcolatrice.
Calcoliamo il rapporto di due lati corrispondenti AB:BC, che sono, ad esempio, l'altezza della statua m. 6 e quella del modello m. 1,20. Osserviamo che tutte le parallele a BC mantengono un valore costante nel rapporto con il corrispondente in AB: ciò significa che tutte le misure prese dal modello mantengono,in proporzione, lo stesso costante rapporto di similitudine. Infatti m. 6: 1,20 = 5, che è il quoto costante di ogni rapporto di similitudine: per cui una misura dal modello es. di cm 70 sarà cm. 70x 5 = cm 350 che dovrà essere riportata sul blocco. Ma in che modo? Negli esempi precedenti, abbiamo ridotto il triangolo di proporzione di 1/3 o di 1/2; e possiamo dividerlo ancora a seconda delle esigenze lavorative. La soluzione che si propone, di fronte a misure sovra dimensionate, riduce il trasporto delle lunghezze, applicando una tecnica semplice e diretta. Data una statua di m. 6 e di un modello di m. 1.20, si prendono dei compassi grandi( maranghino ) ed un metro a nastro di acciaio, flessometro, che una volta srotolato gli consente di mantenere una certa rigidità, e può ssere utilizzato come se fosse una riga flessibile. Così si comincia così il lavoro:
- si svolge e si fissa il metro , per tutta la lunghezza necessaria a riportare i primi capi-punto: nell'esempio dianzi citato, poco oltre m. 6, per agevolare le misure, 1-2-3-4, iniziali, da prendersi con il maranghino;
- si è detto che il valore del quoziente è 5; perciò ogni misura presa dal modello và moltiplicata per 5. Poniamo sia cm. 73, avremo una misura di cm. 73 x 5 = cm 367,5, che con l'apertura del maranghino la prenderemo sul metro.
Si è già accennato al trasporto, a rovescio, di un punto dal marmo al modello, utilizzando la larghezza esistente ( partendo quasi fatti, se il materiale da togliere non è eccessivo ). Con questa tecnica, tutto è molto più facile: supponiamo, a mò di esempio, che la distanza tra il 3° e 4° punto, la larghezza, sia, nel blocco, di cm 275; fatte le dovute intersezioni, se riportiamo il 4° capo-punto sul modello, non abbiamo che da dividere per 5 ( cm 275 : 5 = cm 55 ). Il capo-punto 4 può essere fissato direttamente sul " gesso", oppure su un frammento di "marmetta", allineato sul rettangolo perimetrale, che è segnato intorno al modello come una cornice, nel contesto delle linee e dei supporti (capi-punto ). Il rettangolo prefigura, in proporzione, lo stesso parallelepipedo ( la sua base ) delineato dal marmo. Quindi, compatibile con le distanze del perimetro già definite intorno al modello. Se non vi sono queste condizioni, troppa "roba ", si toglie il marmo necessario.

L'UTILIZZO DELLA CALCOLATRICE
Si è accennato ai numeri interi ed infinitesimali come quoto, è raro che non si possa aggiungere o togliere qualche centimetro per calcolare un numero intero ( es. cm 605 : 121 = 5; oppure cm 601 : 120,2 = 5 ); ma quando ciò non è possibile, non cambia nulla, poichè sono due grandezze omogenee ( uniformi ). In questo esempio, cm 601 : 120 = 5.008333333: il quoto divide e moltiplica, nella stessa maniera, come indicato in quelli precedenti. Se vi sono dubbi o difficoltà si può sempre effettuare un semplice controllo, con il supporto grafico dei triangoli sotto dimensionati, ridotti ad un 1/3 o 1/2, già menzionati nel capitolo precedente.